Usage example: Euler characteristic curves

This notebook provides usage examples for the euchar.curve module.

  • Euler characteristic curves of 2D and 3D images with values sampled from uniform distributions.

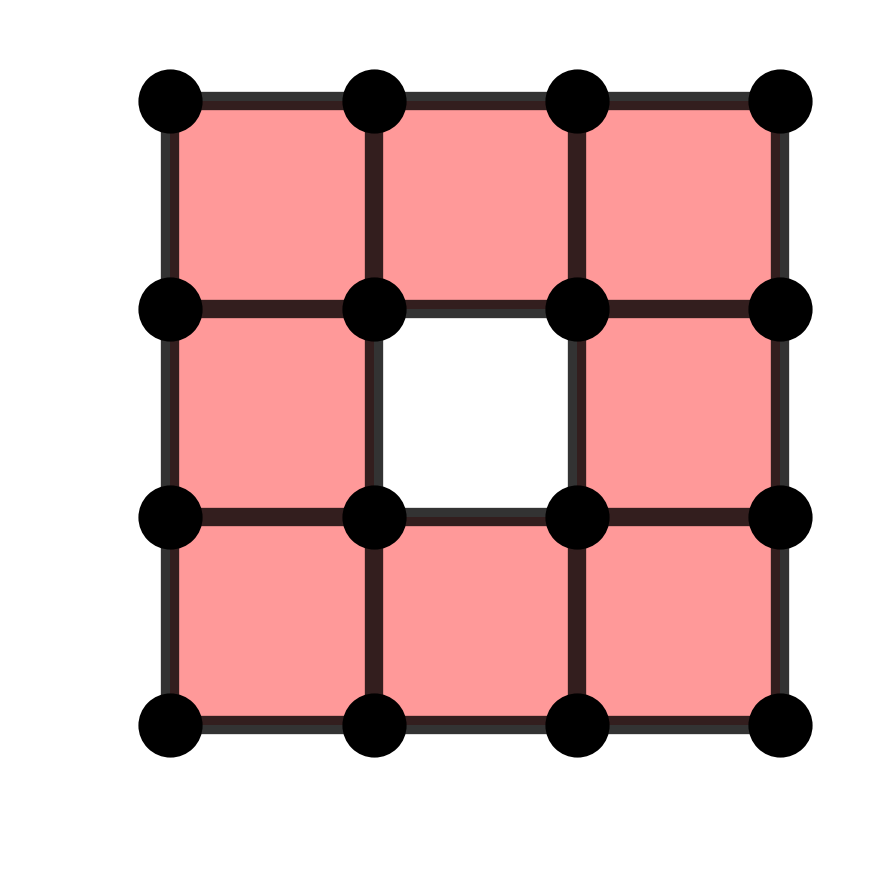
  • Euler characteristic curves of finite point sets in \(\mathbb{R}^2\) and \(\mathbb{R}^3\), obtained using the Alpha filtrations on the finite point sets

import numpy as np

import euchar.utils
from euchar.curve import image_2D, image_3D, filtration
from euchar.filtrations import alpha_filtration_2D, alpha_filtration_3D, inverse_density_filtration
from euchar.display import piecewise_constant_curve

import matplotlib.pyplot as plt
plt.style.use("seaborn-whitegrid")
plt.rcParams.update({"font.size": 16})
from seaborn import distplot

Synthetic data

Images

np.random.seed(0)
m = 32
max_intensity = 256

img_2D = np.random.randint(0, max_intensity, size=(m, m))
img_3D = np.random.randint(0, max_intensity, size=(m, m, m))

Finite point sets

np.random.seed(0)
N = 100
points_2D = np.random.rand(N, 2)
points_3D = np.random.rand(N, 3)

Euler characteristic curves of 2D and 3D image

For the following computation, the vector_2D_changes is automatically computed by image_2D().

ecc_2D = image_2D(img_2D)

To avoid recomputing it every time, it can be passed as a parameter to image_2D().

Precompute it with

vector_2D_changes = euchar.utils.vector_all_euler_changes_in_2D_images()

For the following computation, the vector of all possible Euler changes in the case of 3D images needs to be precomputed and saved to a file.

For example one could do this by running

vector_3D_changes = euchar.utils.vector_all_euler_changes_in_3D_images()
np.save("vector_3D_changes.npy", vector_3D_changes)

vector_3D_changes = np.load("vector_3D_changes.npy")
ecc_3D = image_3D(img_3D, vector_3D_changes)

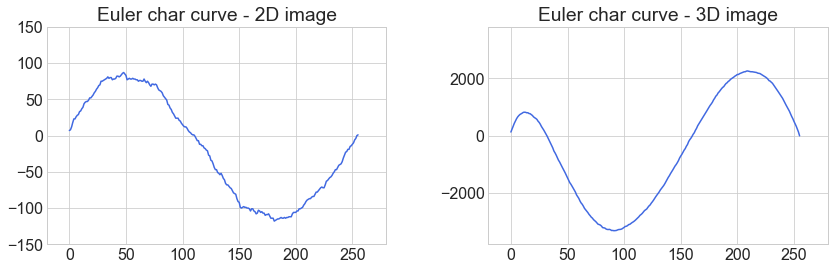
We can then plot the Euler characteristic curves as piecewise constant curves.

fig, ax = plt.subplots(1, 2, figsize=(14,4))
plt.subplots_adjust(wspace=0.3)

domain = np.arange(256)
ax[0].plot(domain, ecc_2D, color="royalblue")
ax[0].set(title="Euler char curve - 2D image", xlim=[-20, 280], ylim=[-150, 150])
ax[1].plot(domain, ecc_3D, color="royalblue")
ax[1].set(title="Euler char curve - 3D image", xlim=[-20, 280], ylim=[-3_800, 3_800]);
../_images/output_17_0.png

Euler characteristic curves of finite point sets

We obtain the Alpha filtrations in the form of arrays of indices of points_2D and points_3D.

simplices_2D, alpha_2D = alpha_filtration_2D(points_2D)
simplices_3D, alpha_3D = alpha_filtration_3D(points_3D)

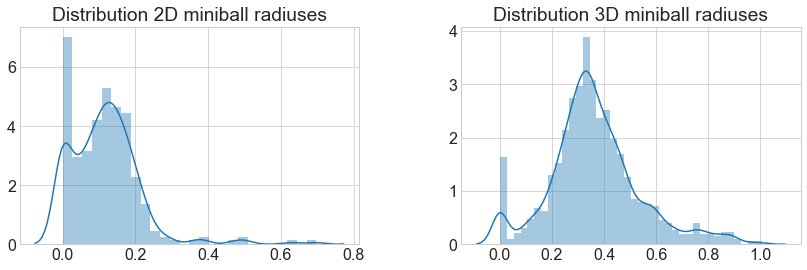
fig, ax = plt.subplots(1, 2, figsize=(14,4))
plt.subplots_adjust(wspace=0.3)
_ = distplot(alpha_2D, ax=ax[0])
ax[0].set(title="Distribution 2D miniball radiuses")
_ = distplot(alpha_3D, ax=ax[1])
ax[1].set(title="Distribution 3D miniball radiuses");
../_images/output_21_0.png

We produce arrays bins_2D and bins_3D, used to discretize the domains of the distributions of 2D and 3D Alpha parametrizations.

bins_2D = np.linspace(0.0, 0.8,  num=200)
filt_2D = filtration(simplices_2D, alpha_2D, bins_2D)

bins_3D = np.linspace(0.0, 1, num=200)
filt_3D = filtration(simplices_3D, alpha_3D, bins_3D)

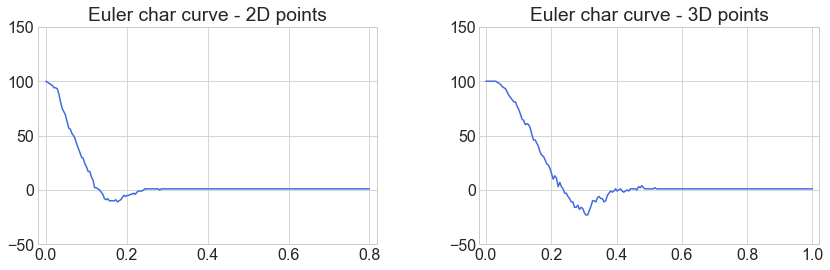
We plot the resulting Euler characteristic curves as piecewise constant curves.

fig, ax = plt.subplots(1, 2, figsize=(14,4))
plt.subplots_adjust(wspace=0.3)

ax[0].plot(bins_2D, filt_2D, color="royalblue")
ax[0].set(title="Euler char curve - 2D points", xlim=[-0.02, 0.82], ylim=[-50, 150])
ax[1].plot(bins_3D, filt_3D, color="royalblue")
ax[1].set(title="Euler char curve - 3D points", xlim=[-0.02, 1.02], ylim=[-50, 150]);
../_images/output_25_0.png